大雾下公式合集

发表于 2021-10-13 更新于 2022-12-05 Waline：阅读次数：

rev0.3.1

Disclaimer

本文档照例应用于考前记诵

但现在内容多得已经可以用来饱和式学习了

本文强调值的运算矢量性时利用箭头符号 \(\vec a\)，描绘一般原则时则使用加粗体 \(\mathbf a\)

所有常量均使用正体（如玻尔兹曼常量 \(\mathrm k\)）

电子电量 \(\mathrm e\) 与自然底数 \(\mathrm e\) 写法一致，但易于从上下文判断

rev 0.1，波动光学还没完善好！

rev 0.2，差不多该可以用了，但也快要考试了，加了一些没什么用的东西

rev 0.3，修正了一些已知错误

rev 0.3，修正了一些微不足道的错误，增加了“平均自由程”

Waiver

采用 cc-by-nc-sa 4.0

不完全对本文摘要内容的严谨性与正确性负责

数学基础

积化和差与和差化积

请不要尝试记住 8 个公式，反之（在考场上）启发式地从以下二式推导 \[ \begin{align} \cos(\alpha + \beta) &+ \cos(\alpha - \beta) \nonumber \newline &= \cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta) + \cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) \nonumber \newline &= 2\cos(\alpha)\cos(\beta) \nonumber \newline \sin(\alpha+\beta) &+ \sin(\alpha - \beta) \nonumber \newline &= \sin(\alpha)\cos(\beta) + \sin(\beta)\cos(\alpha) + \sin(\alpha)\cos(\beta) - \sin(\beta)\cos(\alpha) \nonumber \newline &= 2\sin(\alpha)\cos(\beta) \nonumber \end{align} \]

旋转矢量法解二阶线性微分方程

类似相量法，设复位移 \(x=A\mathrm e^{\mathrm i(\omega t+\phi)}\) 的实部表示位移，则微分关系

\[ \begin{align} \frac{\mathrm d}{\mathrm dt} x &= \mathrm i\omega A \mathrm e^{\mathrm i(\omega t+\phi)} = \omega A \mathrm e^{\mathrm i(\omega t+\phi+\frac{\pi}{2})} \nonumber\newline \frac{\mathrm d^2}{\mathrm dt^2} x &= -\omega^2 A \mathrm e^{\mathrm i(\omega t+\phi)} = \omega^2 A \mathrm e^{\mathrm i(\omega t+\phi+\pi)}\nonumber \end{align} \]

将复位移转化为极坐标形式 \(\vec x=A\angle\phi\)，微分算符几何意义

\[ \begin{align} \frac{\mathrm d}{\mathrm dt} = \omega\angle\frac{\pi}{2} \nonumber\newline \frac{\mathrm d^2}{\mathrm dt^2} = \omega^2\angle\pi \nonumber \end{align} \]

谐振子

微分方程 \[ -kx + F_0\cos(\omega t) = m\frac{\mathrm d^2}{\mathrm dt^2}x + \mu\frac{\mathrm d}{\mathrm dt}x \] 其中驱动力项 \(F_0\cos(\omega t)\)，阻尼项 \(\mu\frac{\mathrm d}{\mathrm dt}x\)，恢复力项 \(-kx\)

旋转矢量形式 \[ -kA\angle\phi+F_0\angle0=m\omega^2 A\angle(\pi+\phi)+\mu\omega A\angle(\frac{\pi}{2}+\phi) \] 画图求解即可

结论： \[ \begin{align} \omega_0 &= \sqrt\frac{k}{m} \nonumber\newline n&=\frac{\mu}{2m} \nonumber\newline f &= \frac{F_0}{m} \nonumber\newline A &= \frac{f}{\sqrt{(\omega_0^2-\omega^2)^2+4n^2\omega^2}} \nonumber\newline \tan\phi &= \frac{2n\omega}{\omega_0^2-\omega^2}\nonumber \end{align} \]

热力学

状态方程

\[ \begin{align} pV=\nu \mathrm R T \nonumber\newline p = n\mathrm k T \nonumber \end{align} \]

其中 \(\nu\) 为物质的量（摩尔数），\(n\) 为分子数密度，\(\mathrm k = \frac{\mathrm R}{\mathrm {N_A}}\)

微观状态量

分子平均平动动能

\[ \overline\varepsilon \triangleq \frac{1}{2}m_0\overline{v^2} = \frac{3}{2}\mathrm k T \]

其中 \(m_0\) 为分子质量，由状态方程可得 \(p = \frac{2}{3}n\overline\varepsilon\)

麦克斯韦分布

\[ f(v) = 4\pi\left(\frac{m_0}{2\pi\mathrm k T}\right)^{\frac{3}{2}}v^2\mathrm e^{-\frac{m_0v^2}{2\mathrm kT}} \]

平均速率 \(\overline v\)	方均根速率 \(\sqrt{\bar {v^2}}\)	最概然速率 \(v_p\)
\(\sqrt{\frac{8}{\pi}}\sqrt{\frac{\mathrm RT}{M}}\)	\(\sqrt{3}\sqrt{\frac{\mathrm RT}{M}}\)	\(\sqrt{2}\sqrt{\frac{\mathrm RT}{M}}\)

其中 \(M=m_0 \mathrm {N_A}\) 为分子量（注意单位 \(\mathrm{g\cdot mol^{-1}}\)）

玻尔兹曼分布

\[ n=n_0 \mathrm e^{-\frac{\varepsilon_p}{\mathrm k T}} \]

平均自由程

平均碰撞频率 \(\overline Z\)

\[ \overline Z = \sqrt{2}n\pi d^2\overline v \] 其中 \(d\) 为分子直径

平均自由程 \(\overline \lambda\)

\[ \overline \lambda=\frac{1}{\sqrt{2}\pi d^2n}=\frac{\mathrm kT}{\sqrt{2}\pi d^2p} \]

内能

\[ E = \nu \frac{i}{2}\mathrm R T \]

其中 \(i\) 为分子自由度

热容

等体摩尔热容 \(C_{V,m}=\frac{i}{2}\mathrm R\)

等压摩尔热容 \(C_{p,m}= C_{V,m} + R =\frac{i+2}{2}\mathrm R\)

摩尔热容比 \(\gamma \triangleq \frac{C_{p,m}}{C_{V,m}} = \frac{i+2}{i}\)

热力学第一定律

\[ Q = \Delta E + A \]

其中 \(Q\) 为系统向外界吸热，\(\Delta E = E_2-E_1\) 为系统内能增量，\(A\) 为系统对外做功

热机

热机效率

\[ \eta \triangleq \frac{A}{Q_1} \]

其中 \(A\) 为热机循环对外做功，\(Q_1\) 为系统向高温热源吸热

当热机为卡诺热机或可逆热机时， \(\eta = \eta_{\text{max}}=1-\frac{T_2}{T_1}\)，其中 \(T_1\)，\(T_2\) 分别为高温、低温热源温度

致冷效率

\[ \omega = \frac{Q_2}{A} \]

其中 \(A\) 为外界对致冷机做功，\(Q_2\) 为系统向低温冷库吸热，\(\omega_\text{max} = \frac{T_2}{T_1-T_2}\)

热力学第二定律

\(\eta < 1\)，并有 \(\omega \neq +\infty\)

熵

在可逆过程中有

\[ \mathrm d S=\frac{\mathrm d Q}{T} \] 其中 \(Q\) 为进入系统的热量

热力学第三定律

\(T=0 \ \mathrm K\) 时有 \(S = 0\)

过程公式

过程	特征方程	\(Q\)	\(A\)	\(\Delta E\)
等体过程	\(V=V_0\)	\(\nu C_{V,m}\Delta T\)	\(0\)	\(=Q\)
等压过程	\(p=p_0\)	\(\nu C_{p,m}\Delta T\)	\(p\Delta V\)	\(\nu C_{V,m}\Delta T\)
等温过程	\(pV=p_0V_0\)	\(\nu \mathrm R T\ln\frac{V_2}{V_1}\)	\(=Q\)	\(0\)
绝热过程	\(pV^\gamma=p_0V_0^\gamma\)	\(0\)	\(=-\Delta E\)	\(\nu C_{V,m}\Delta T\)
多方过程	\(pV^n=p_0V_0^n\)

机械波

miscellaneous

频率 \(\nu\)，周期 \(T\)，波速 \(u\)，波长 \(\lambda\)，频率 \(f\)，圆频率 \(\omega\)，振幅 \(A\)

\[ \begin{align} \nu = \frac{1}{T} \nonumber\newline u = \frac{\lambda}{T} = \nu\lambda \nonumber\newline \omega = 2\pi f = \frac{2\pi}{T} \nonumber \end{align} \]

平面简谐波方程

\[ y(x,t)=A\cos\left(\omega\left(t-\frac{x}{u}\right)+\phi_0\right) \]

其中 \(y\) 表示 \(x\) 处质点偏离平衡位置的位移

波动微分方程

\[ \frac{\partial^2 y}{\partial x^2}=\frac{1}{u^2}\frac{\partial^2 y}{\partial t^2} \]

波状态量

波能量

设质点 \((x,t)\) 处小段质元 \(\Delta x\) 的动能为 \(E_k\)，势能为 \(E_p\) \[ E_k=E_p=\frac{1}{2}\rho\Delta x A^2\omega^2\sin^2\left[\omega\left(t-\frac{x}{u}\right)+\phi_0\right]=\frac{1}{2}\rho\Delta x \omega^2 y_{\phi}^2 \] 其中 \(y_\phi\) 表示以 \(\frac{\pi}{2}\) 相位超前 \(y\) 的位移，\(\rho\) 为质量密度

能量密度

单位体积中波的能量 \[ w = \frac{E}{\Delta V}=\frac{E_k+E_p}{\Delta x\Delta S} = \rho\omega^2 y_{\phi}^2 \] 其中 \(V\) 为体积，\(S\) 为对于平面波所考虑的面积

平均能量密度

\[ \overline w = \frac{1}{2}\rho A^2\omega^2 \]

能流密度/波强

\[ \vec I\triangleq \overline w\vec u =\frac{1}{2}\rho A^2\omega^2\vec u \]

波功率/非平面波振幅

\[ P = \vec I\cdot\vec S \]

在取 \(\vec S /\kern -0.3 em/ \vec u\) 时可不考虑矢量性，利用波功率守恒可推导出非平面波振幅（平方与面积反比）

波的吸收

即波功率的吸收

\[ \begin{align} \mathrm d I &= -\alpha I \mathrm d x \nonumber\\ I&=I_0\mathrm e^{-\alpha x} \nonumber \end{align} \]

波的合成

相干波

频率相同
振动方向相同
相位差恒定

设两波相位差为 \(\Delta\phi=(\phi_2-\phi_1)-2\pi\frac{r_2-r_1}{\lambda}\)，合成波满足 \[ A^2=A_1^2+A_2^2+2A_1A_2\cos\Delta\phi \] \(A_\text{max} =A_1+A_2 \Rightarrow I_\text{max} = I_1+I_2+2\sqrt{I_1I_2}\)

\(A_\text{min} =\left|A_1-A_2\right| \Rightarrow I_\text{min} = I_1+I_2-2\sqrt{I_1I_2}\)

驻波

固定端反射存在半波损失（反射点必为波节） \[ \begin{align} y&=y_1+y_2=A\left[\cos2\pi\left(\nu t-\frac{x}{\lambda}\right) + \cos2\pi\left(\nu t+\frac{x}{\lambda}\right) \right] \nonumber \newline &= 2A\cos\left(2\pi\frac{x}{\lambda}\right)\cdot\cos2\pi\nu t \nonumber \end{align} \]

拍频波

圆频率相近（\(|\omega_1-\omega_2|\ll \omega_1\)）的两列振动方向相同波合成（利用和差化积推导）

合成波振幅（包络）的圆频率 \(\omega=\left|\frac{\omega_1-\omega_2}{2}\right|\)

拍频 \(f = \left|f_1-f_2\right|\)，为两个振幅峰值出现频率

振动方向垂直的波合成

利用李萨如图形分析

多普勒效应

设波速率 \(u\)，波源相对介质速度为 \(\vec v_s\)，观察者相对介质速度 \(\vec v_0\)，波源相对观察者位移单位向量 \(\vec r_0=\frac{\vec r}{|\vec r|}\)

原频率 \(\nu_0\) 与观察频率 \(\nu\) 的关系

\[ \nu = \frac{u + \vec v_0 \cdot \vec r_0}{u+\vec v_s\cdot \vec r_0}\nu_0 \] 若观察者相对波源速度平行且相反

\[ \nu = \frac{u+v_0}{u-v_s}\nu_0 \]

马赫锥

\[ \sin\theta = \frac{u}{v_s} \]

波动光学

光强

\[ \mathbf I=\left<\mathbf S\right>=\left<\mathbf{E\times H}\right> \propto \frac{1}{2}E_0^2 \]

其中坡印廷矢量 \(\mathbf S=\mathbf{E\times H}\)，\(\mathbf E\)，\(\mathbf H\) 分别为电场强度矢量，磁场强度矢量，\(E_0\)，\(H_0\) 为其振幅

有 \(\sqrt{\varepsilon_0}E_0=\sqrt{\mu_0}H_0\)，光速 \(\mathrm c=\sqrt{\frac{1}{\varepsilon_0\mu_0}}\)，\(\varepsilon_0\) 为真空电介常数，\(\mu_0\) 为真空磁介常数

算符 \(\left<\right>\) 为平均算符

相干性

空间相干性

光源线度对相干性的影响 \[ b = \frac{B}{d}\lambda \] 其中 \(b\) 为光源线度，\(B\) 为光源与双缝的距离（观测距离），\(d\) 为双缝间距（相干性度量）

时间相干性

\[ L=\frac{\lambda^2}{\Delta \lambda} \]

\(L\) 表示相干长度，\(\Delta \lambda\) 为单色性的度量

光的干涉

干涉条纹条件

\[ \delta(x) = \begin{cases} \pm 2k\cdot\frac{\lambda}{2} &, & k \in \mathbb{N}_+ &, \text{ center of light stripes} \newline \pm (2k+1)\cdot\frac{\lambda}{2} &, & k \in \mathbb{N} &, \text{ center of dark stripes} \end{cases} \]

其中 \(\delta(x)\) 为使用分波阵面法或分振幅法时，在成像位置 \(x\) 形成的光程差

举例

以下举例不同干涉实验中光程差的具体计算

双缝干涉

当缝宽度 \(a \ll\) 双缝间距 \(d\) 时

\[ \delta = \frac{xd}{D} \] 其中 \(D\) 为光屏与双缝距离，\(D \gg d\) 或 \(D= f\)（凸透镜汇聚）

劈尖干涉/牛顿环/薄膜干涉/迈克尔逊干涉仪

设单色光以入射角 \(\gamma\) 入射折射率为 \(n_2\) 的材料，入射处厚度为 \(d\)

假设入射方向观察干涉对象（反射光干涉），且环境折射率 \(n_1 < n_2\)，一次反射光有半波损失，则

\[ \delta = 2n_2d\cos\gamma + \frac{\lambda}{2} \] 若光源（可近似）为平行光，即关注 \(d\) 对 \(\delta\) 的影响时，形成等厚干涉条纹：同一条纹厚度相等，形成“等高线”

若光源（可近似）为无限大面光源，即关注 \(\gamma\) 对 \(\delta\) 的影响时，形成等倾干涉条纹：同一条纹倾角相等

牛顿环入射处厚度近似

设凸透镜曲率半径 \(R\)，条纹距接触点距离 \(r\)，该位置空气隙厚度 \(d\)，有 \[ R^2=r^2+(R-d)^2=r^2+R^2-2Rd+d^2 \] 由于 \(d \ll R\)，\(d^2 \ll Rd \ll R^2\)，则 \[ d = \frac{r^2}{2R} \]

迈克尔逊干涉仪

可以同时体现等厚、等倾干涉的仪器，有

\[ \delta = 2d \] 其中 \(d\) 为反射镜 \(M_1\) 与 \(M_2'\)（\(M_2\) 关于分光板 \(G_1\) 的像）在反射位置的距离

衍射的干涉化处理

半波带法

可以利用“半波带法”将单缝夫琅禾费衍射以干涉形式计算

设单缝衍射缝宽 \(a\)，考虑衍射角（与法向夹角）为 \(\phi\) 的出射光线

将波面分为宽度为 \(\Delta S\) 的窄条，使得窄条上下光线相位差为 \(\pi\)

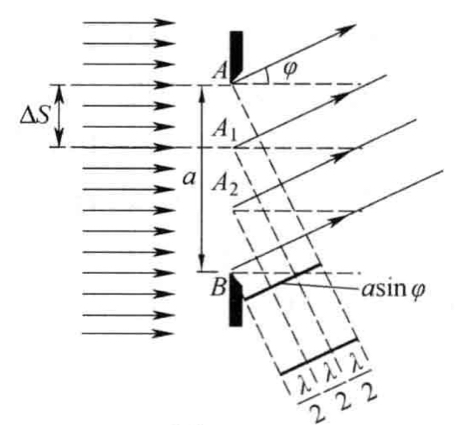
半波带数量 \(N = \frac{a\sin\phi}{\frac{\lambda}{2}}\)，则当 \(N\) 为奇数时明纹，偶数时暗纹，此结论形式上与将

\[ \delta=a\sin\phi \] 代入干涉条件时一致

半波带法的局限

由菲涅尔积分法，得到暗纹条件一致，真实明纹条件 \(\phi\) 略小于半波带法的结果

设 \(\alpha = \frac{\pi a\sin\phi}{\lambda}\)，有次极大条件 \(\tan\alpha=\alpha\)

设中央明纹亮度 \(I_m\)，有 \(I = I_m\left(\frac{\sin\alpha}{\alpha}\right)\)

光栅

干涉成分

假设光在每缝的衍射是均匀的，考虑干涉条纹

设光栅缝（透光部分）宽 \(a\)，不透光部分宽度 \(b\)，光栅常量 \(d = a + b\)，缝总数 \(N\)，平行光以于光栅法线夹角 \(\theta\) 斜入射，考虑衍射角为 \(\phi\) 的衍射光

光栅明纹方程 \[ d(\sin\phi+\sin\theta)=\pm k\lambda\ ,\ k = 0, 1, 2,\cdots \] 其中 \(k\) 称为“明纹级数”

次极大光强分布

利用振幅矢量法推导，存在次极大 \[ Nd(\sin\phi+\sin\theta)=\pm m\lambda \]

考虑衍射时，设 \(\delta\) 为相邻两光线相位差 \[ I = I_m\left(\frac{\sin\alpha}{\alpha}\right)^2\left(\frac{\sin\frac{N\delta}{2}}{\sin\frac{\delta}{2}}\right)^2 \]

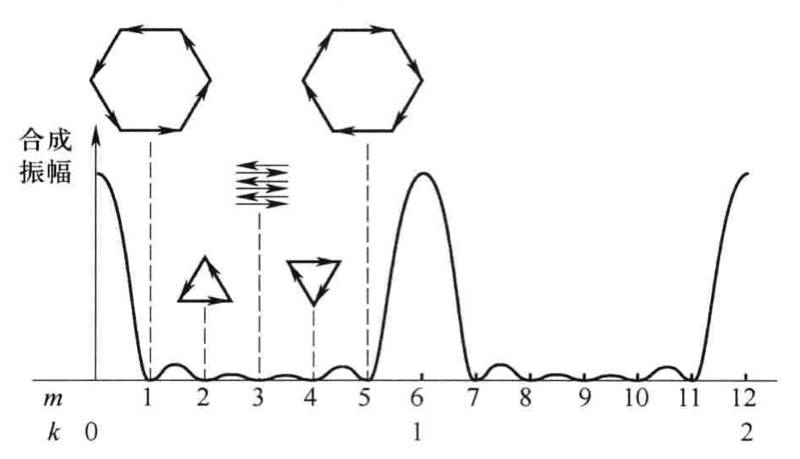
衍射成分

造成了光栅条纹的“缺级”，当

\[ \frac{a}{a+b}k=k'\ ,\ k' = 1,2,\cdots \] 或 \[ k = \frac{a+b}{a}k' \] 时，第 \(k\) 级明纹不存在

光学系统最小分辨角

\[ \phi = 1.22\frac{\lambda}{D} \]

其中 \(\phi\) 为最小分辨角，\(D\) 为光学系统孔径

偏振光

马吕斯定律

\[ I=I_0\cos^2\alpha \]

其中 \(\alpha\) 为两偏振片偏振化方向夹角

布儒斯特定律

以入射角 \(i\) 由介质折射率 \(n_1\) 入射晶体 \(n_2\) 的自然光，当反射光垂直于折射光时入射角为 \(i_b\)，此时反射光为线偏振光，且偏振化方向垂直于主平面

\[ \tan i_b=\frac{n_2}{n_1} \]

晶体双折射

o 光：波阵面各向同性，折射率 \(n_o\)，偏振化方向垂直于自身主平面
e 光：波阵面各向异性，折射率 \(n_e\)，偏振化方向在自身主平面内

\(n_e > n_o\) 正晶体，反之负晶体

光轴

o 光与 e 光波阵面同向的方向

垂直于光轴入射时，e 光偏振化方向平行光轴，o 光偏振化方向垂直光轴

分离两类光

尼科尔棱镜：加拿大树胶可使 o 光全反射
沃拉斯顿棱镜：两个光轴方向垂直的双折射晶体

偏振干涉

利用偏振片将两个出射光成分调整至同一偏振化方向形成干涉的现象，\(d\) 为波片厚度

\[ \delta=\frac{2\pi}{\lambda}\left|n_o-n_e\right|d + \Delta\phi \] 当利用偏振片调整后两偏振化方向相反时有 \(\Delta\phi=\pi\)

近代物理

相对论

基本公式

\(\beta = \frac{v}{\mathrm c}\)

能量 \(E = m\mathrm c^2\)

相对论质量 \(m = \frac{m_0}{\sqrt{1-\beta^2}}\)

动能 \(E_k = m\mathrm c^2 - m_0\mathrm c^2\)

动量 \(\vec p = m\vec v=\frac{m_0}{\sqrt{1-\beta^2}} \vec v\)

洛伦兹变换

设参考系 \(S'\) 相对 \(S\) 以速度 \(\vec u = (u, 0, 0)\) 运动，则原参考系 \(S\) 下坐标 \((x, y, z)\)，与变换参考系 \(S'\) 下坐标 \((x',y',z')\) 满足：

\[ \begin{cases} & x' & = & \frac{x-ut}{\sqrt{1-\beta^2}} \newline & y' & = & y \newline & z' & = & z \newline & t' & = & \frac{t-\frac{u}{\mathrm c^2}x}{\sqrt{1-\beta^2}} \end{cases} \ \ \ \ \ \ \ \ \begin{cases} & x & = & \frac{x'+ut}{\sqrt{1-\beta^2}} \newline & y & = & y' \newline & z & = & z' \newline & t & = & \frac{t'+\frac{u}{\mathrm c^2}x'}{\sqrt{1-\beta^2}} \end{cases} \]

速度变换

设 \(\xi = 1-\frac{u}{\mathrm c^2}v_x\)，\(\eta = 1+\frac{u}{\mathrm c^2}v_x'\)

\[ \begin{cases} & v_x' & = & \frac{v_x-u}{\xi} \newline & v_y' & = & \frac{v_y\sqrt{1-\beta^2}}{\xi} \newline & v_z' & = & \frac{v_z\sqrt{1-\beta^2}}{\xi} \newline \end{cases} \ \ \ \ \ \ \ \ \begin{cases} & v_x & = & \frac{v_x'+u}{\eta} \newline & v_y & = & \frac{v_y'\sqrt{1-\beta^2}}{\eta} \newline & v_z & = & \frac{v_z'\sqrt{1-\beta^2}}{\eta} \newline \end{cases} \]

量子物理

黑体辐射

斯特藩-玻尔兹曼定律

\[ M_B(T)=\int_0^{+\infty} M_B(T,\lambda) \mathrm d \lambda = \sigma T^4 \]

其中 \(M_B\) 为黑体辐出度，\(\sigma = 5.670373\times10^{-8}\ \mathrm{Wm^{-2}K^{-4}}\) 为斯特藩-玻尔兹曼常量

维恩位移定律

\[ T\lambda_m = \mathrm b \]

其中 \(\lambda_m\) 表示峰值波长，\(\mathrm b = 2898 \ \mathrm{\mu m\cdot K}\) 为一常数

普朗克公式

\[ M_B(T,\lambda)=\frac{2\pi\mathrm {hc^2}\lambda^{-5}}{\mathrm e^{\frac{\mathrm {hc}}{\lambda\mathrm k T}} - 1} \]

光电效应

爱因斯坦光电效应方程

\[ \mathrm h\nu = A+\frac{1}{2}mv_m^2 \]

其中 \(A\) 为逸出功，\(\frac{1}{2}mv_m^2\) 为电子的最大初动能

可得截止频率 \(\nu_0=\frac{A}{\mathrm h}\)，遏止电压 \(U_a=\mathrm{\frac{h}{e}}\nu - \mathrm{\frac{A}{e}}\)，其中 \(\mathrm e\) 为电子电量

康普顿散射

\[ \Delta \lambda = \lambda -\lambda_0=\mathrm{\frac{h}{m_0c}}(1-\cos\theta) \]

其中 \(\mathrm {m_0}\) 为电子静质量，\(\lambda\) 为散射波波长，\(\lambda_0\) 为入射光波长

初步原子模型

里德伯-里兹并合原则

\[ \sigma=\frac{1}{\lambda}=\mathrm{R_H}\left(\frac{1}{k^2}-\frac{1}{n^2}\right)\ ,\ n>k\in\mathbb{Z}_+ \]

其中 \(\sigma\) 称为波数，里德伯常量 \(\mathrm{R_H}=1.0973731\times10^{-7}\ \mathrm{m^{-1}}\)

玻尔氢原子模型

定态假设 \(E = E_n= -\frac{1}{n^2}\left(\frac{m\mathrm e^4}{8\varepsilon_0^2\mathrm h^2}\right)\ ,\ n\in \mathbb{Z}_+\)
辐射频率公式 \(\nu_{kn}=\frac{|E_k-E_n|}{\mathrm h}\)
角动量量子化条件 \(L = mvr = n\frac{\mathrm h}{2\pi}= n\hbar\ ,\ n\in\mathbb{Z}_+\)
定态轨道半径 \(r_n=n^2\left(\frac{\varepsilon_0\mathrm h^2}{\pi m\mathrm e^2}\right) = n^2r_1\ ,\ n\in\mathbb{Z}_+\)

索末菲椭圆轨道理论

长半轴 \(a=n^2r_1\)
短半轴 \(b= nn_\phi r_1 = \frac{n_\phi}{n}a\ ,\ n_\phi < n\in\mathbb{Z}_+\)

量子力学原子模型

电子能量量子化 \(E_n=-\frac{1}{n^2}\left(\frac{m\mathrm e^4}{8\varepsilon_0^2\mathrm h^2}\right)\ ,\ n\in \mathbb{Z}_+\)
电子角动量量子化 \(L=\sqrt{l(l+1)}\hbar\)，磁矩 \(\mu = -\mathrm{\frac{e}{2me}}L\)
角动量空间取向量子化 \(L_z=m_l\hbar\)
自旋角动量量子化 \(S=\sqrt{s(s+1)}\hbar = \sqrt{\frac{1}{2}(\frac{1}{2}+1)}\hbar\)，角动量（取向）在 \(z\) 方向分量 \(S_z=m_z\hbar\)

量子数

量子数	符号	取值范围	意义	本层最高容纳电子数
主量子数	\(n\)	\(1, 2, 3, \cdots\)	大体上的能量（壳层）	\(2n^2\)
副量子数	\(l\)	\(0, 1, 2,\cdots,n-1\)	角动量与能量（支壳层）	\(2(2l+1)\)
磁量子数	\(m_l\)	\(0,\pm1,\pm2,\cdots,\pm l\)	角动量的取向	\(2l+1\)
自旋量子数	\(m_s\)	\(\pm\frac{1}{2}\)	电子角动量的取向	\(2\)

德布罗意物质波

动量 \(p=mv=\frac{\mathrm h}{\lambda}\)

能量 \(E=m\mathrm c^2 = \mathrm h\nu\)

不确定性关系

\[ \begin{align} \Delta x\Delta p_x \geq \frac{\hbar}{2} \nonumber\newline \Delta E\Delta t \geq \frac{\hbar}{2} \nonumber \end{align} \]

后者表示能级宽度与能级稳定性的关系

薛定谔方程

\[ \left[V-\frac{\hbar}{2m}\Delta\right]\Psi=\mathrm i\hbar\frac{\partial\Psi}{\partial t} \]

其中波函数 \(\Psi(\vec r,t)\) 满足单值、有限、连续且有平方归一化条件

拉普拉斯算子 \(\Delta=\nabla\cdot\nabla=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\)

\(V(\vec r,t)\) 为空间势函数

定态薛定谔方程

在粒子总能量 \(E=V+\frac{p^2}{2m}\) 不随 \(t\) 变化的条件下，有分离变量形式 \(\Psi(\vec r,t)=\Psi(\vec r)\mathrm e^{-\frac{2\pi\mathrm i}{\mathrm h} Et}\)，则

\[ \Delta\Psi+\frac{2m}{\hbar^2}(E-V)\Psi=0 \]

一维无限深势阱

\[ \begin{cases} & V(x) & = & 0 &, & x\in(0, a) \newline & V(x) & = &\infty &, & x\in(-\infty,0]\cup[a,+\infty) \end{cases} \]

一维定态薛定谔方程的解：

\[ \Psi_n(x)=\pm\sqrt{\frac{2}{a}}\sin\frac{n\pi}{a}x\ ,\ n=1,2,3,\cdots \] 能量 \(E_n=n^2\frac{\mathrm h^2}{8ma^2}\)

驻波条件 \(a=n\frac{\lambda_n}{2}\)

激光与固体物理

格波

声子能量 \(E=\hbar\omega\)，其中 \(\omega\) 为格波角频率

固体能带

原子能级分裂数 \(N\) 为晶体原子数，形成满带、禁带、空带（导带）、价带（导带）

导体

存在价带/空带满带重叠/价带空带重叠

绝缘体

满带与最近空带间禁带宽度 \(\Delta E_g=3\sim6\ \mathrm{eV}\)

半导体

满带与最近空带间禁带宽度 \(\Delta E_g=0.1\sim1.5\ \mathrm{eV}\)

n 型半导体：掺入五价元素（砷 As、磷 P、锑 Sb）
p 型半导体：参入三价元素（硼 B、镓 Ga、铟 In、铝 Al）

激光原理

玻尔兹曼分布

设系统热平衡状态温度 \(T\) 下处于能级 \(i\) 的原子数为 \(N_i\) \[ N_i \propto g_i e^{-\frac{E_i}{\mathrm kT}} \] 其中 \(g_i\) 为该能级的简并数

粒子数反转：高能级原子数大于低能级原子数的现象

自发辐射系数

\[ \left(\frac{\mathrm dN_{21}}{\mathrm dt}\right)_{\text{ spontaneous}} = A_{21}N_2 \]

其中 \(N_{21}\) 为能级 \(2\) 转移至能级 \(1\) 的粒子数，\(A_{21}\) 为自发辐射系数

受激辐射系数

\[ \left(\frac{\mathrm dN_{21}}{\mathrm dt}\right)_{\text{ motivated}} = kN_2IB \]

其中 \(k\) 为比例系数，\(I\) 为激发光强，\(B\) 为受激辐射系数

受激吸收系数

\[ \left(\frac{\mathrm dN_{12}}{\mathrm dt}\right)_{\text{ motivated}} = kN_1IB' \]

其中 \(k\) 为比例系数，\(I\) 为激发光强，\(B'\) 为受激吸收系数，简并度相同时 \(B'=B\)

光增益

光在经过增益介质时光强 \(I\) 随经过距离 \(z\) 的变化

\[ \mathrm dI(z)=GI(z)\mathrm dz \] 或 \[ I(z)=I_0\mathrm e^{Gz} \] 其中 \(G\) 为光增益系数

激光器

设增益介质长度 \(L\)，两反射镜反射率分别为 \(r_1\)，\(r_2\)

阈值条件

\[ r_1r_2\mathrm e^{2GL}\geq 1 \]