概率统计与随机过程复习整理

发表于 2021-10-13 更新于 2022-12-05 Waline：阅读次数：

概率论

不等式合集

柯西-施瓦茨不等式

由协方差性质推导 \[ E\left((XY)^2\right)\leq E(X^2)E(Y^2) \]

马尔可夫不等式

$r$ 阶矩存在，则 $\forall \varepsilon >0$ \[ P\{|X|\geq \varepsilon\}\leq \frac{(|X|^r)}{\varepsilon^r} \]

切比雪夫不等式

\[ \begin{align} P\{|X-E(X)|\geq \varepsilon\}&\leq\frac{D(X)}{\varepsilon^2} \nonumber\newline P\{|X-E(X)|< \varepsilon\}&\geq 1-\frac{D(X)}{\varepsilon^2}\nonumber \end{align} \]

事件

随机现象的观察（随机试验） $E$ 的样本空间为 $\Omega=\{\omega\}$，随机事件 $A\subset \Omega$。必然事件 $\Omega$，不可能事件 $\varnothing$

事件 $A$、$B$ 的和 $A\cup B = A+B$ 表示其中至少一件事情发生

事件 $A$、$B$ 的积 $A\cap B = AB$ 表示均发生

互斥 $AB=\varnothing$

$A$ 的对立 $\overline A$

事件 $A$、$B$ 的差 $A-B=A\overline B$ 表示 $A$ 发生而 $B$ 不发生

交换律、结合律、分配律、对偶律、吸收律、德摩根律

事件的概率

古典概型 $P(A)=\frac{\text{ sum of}A\text{ results}}{\text{ total results}}$
几何概型 $P(A)=\frac{S_A}{S_{\Omega}}$
频数 $f_n(A)=\frac{n_A}{n}$，统计概率 $P(A)=p\sim\lim\limits_{n\to \infty} f_n(A)$

概率的性质

基本性质

$P(A)\geq 0$
$P(\Omega)=1$
设 $A_i$ 两两互斥，$P\left(\bigcup_i A_i\right)=\sum_i P(A_i)$

不可能事件性质 $P(\varnothing)=0$

可减性 $A\subset B \Rightarrow P(B-A)=P(B)-P(A)$

取反性 $P\left(\overline A\right)=1-P(A)$

容斥原理 $P(\bigcup_i A_i)=\sum_{S\subset\{A_i\}}(-1)^{|S|-1}P(\bigcap_{s\in S}s)$

概率的连续性

条件概率

$P(A|B)=\frac{P(AB)}{P(B)}$

若 $B_1,B_2,\cdots$ 构成互斥完备事件组且 $P(B_i)>0$

全概率公式 \[ P(A)=\sum_j P(B_j)P(A|B_j) \] 贝叶斯公式 \[ P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\sum_j P(B_j)P(A|B_j)}=\frac{P(B_i)P(A|B_i)}{P(A)} \]

独立事件

$A,B$ 独立即 $P(AB)=P(A)P(B)$

$A,B \text{ are independent} \Longleftrightarrow A,\overline B \text{ are independent} \Longleftrightarrow \overline A,B \text{ are independent} \Longleftrightarrow \overline A,\overline B \text{ are independent}$

事件集中事件相互独立，即对所有子集，满足积的概率等于概率的积

随机变量

随机变量 $X$ 为随机试验 $E$ 中随机事件 $\omega$ 的单值实函数

分布函数 $F(x)=P(\{X\leq x\})$，（以后记作 $P\{X\leq x\}$）

连续型随机变量概率密度 $F(x)=\int_{-\infty}^x f(x)\mathrm d x$

多维随机变量

二维连续型随机变量 $(X,Y)$

联合分布函数 $F(x,y)$，联合概率密度函数 $f(x,y)$

边缘概率密度 $f_X(x)=\int_{-\infty}^{+\infty}f(x, y)\mathrm d y$

条件概率密度 $f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$

随机变量独立 $F(x,y)=F_X(x)F_Y(y) f(x,y)=f_X(x)f_Y(y) X,Y $

相互独立随机变量的函数相互独立

随机变量的函数

$y=g(x)$ 严格单调可导时，$Y=g(X)$ 的概率密度

\[ f_Y(y) = \begin{cases} f_X(g^{-1}(y))\left| \frac{\mathrm d g^{-1}(y)}{\mathrm d y} \right| &, y\in \mathscr R(g) \newline 0 &, \text{ else} \end{cases} \]

随机变量和概率密度 $Z=X+Y$（卷积公式） \[ f_Z(z)=\int_{-\infty}^{\infty}f_{XY}(x,z-x)\mathrm dx \xlongequal{X \text{ and } Y \text{ are independent}} \int_{-\infty}^{\infty}f_X(x)f_Y(z-x)\mathrm dx \] 随机变量商概率密度 $Z=X/Y$ \[ f_Z(z)= \int_{-\infty}^{\infty} |y|f_{XY}(yz, y)\mathrm d y \xlongequal{X \text{ and } Y \text{ are independent}} \int_{-\infty}^{\infty} |y|f_X(yz)f_Y(y)\mathrm d y \] 随机变量取最大最小值概率分布 $M=\max_i\{X_i\}$，$N=\min_i\{X_i\}$

\[ \begin{align} F_M(z)=\prod_i F_{X_i}(z) \nonumber\newline F_N(z)=1-\prod_i (1-F_{X_i}(z))\nonumber \end{align} \]

随机变量数字特征

期望

\[ \begin{align} E(X)&=\int_{-\infty}^{+\infty} xf(x)\mathrm d x \nonumber\newline E(g(X)) &= \int_{-\infty}^{+\infty} g(x)f(x)\mathrm d x \nonumber\newline E(g(X,Y)) &= \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} g(x,y)f(x,y)\mathrm d x\mathrm d y \nonumber\newline \end{align} \]

期望是线性的
若随机变量 $X$ 和 $Y$ 独立，$E(XY)=E(X)E(Y)$

方差

\[ D(X)=E\left((X-E(X))^2\right)=E(X^2)-E^2(X) \]

$D(C)=0$
$D(CX)=C^2D(X)$
$D(X\pm Y)=D(X)+D(Y)\pm 2\mathrm{Cov}(X,Y)$

协方差

\[ \mathrm{Cov}(X,Y)=E\left((X-E(X))(Y-E(Y))\right) = E(XY)-E(X)E(Y) \]

$\mathrm{Cov}(aX,bY)=ab\mathrm{Cov}(X,Y)$
$\mathrm{Cov}(X_1+X_2,Y)=\mathrm{Cov}(X_1,Y)+\mathrm{Cov}(X_2,Y)$

矩

$n$ 阶原点矩 $\alpha_n=E(X^n)$

$n$ 阶中心矩 $\mu_n=E\left((X-E(X))^n\right)$

$X,Y$ 的 $k+l$ 阶混合原点矩、混合中心矩

各分布随机变量的形式与特征及关系

离散型随机变量

$X$ 的分布	分布律 $P\{x=k\}$	期望 $E(X)$	方差 $D(X)$
两点分布 $B(n,p)$	$C_n^kp^k(1-p)^{n-k}$	$np$	$np(1-p)$
泊松分布 $P(\lambda)$	$\frac{\lambda^k}{k!}\exp(-\lambda)$	$\lambda$	$\lambda$
几何分布 $G(p)$	$(1-p)^{k-1}p$	$\frac{1}{p}$	$\frac{1-p}{p^2}$

连续型随机变量

$X$ 的分布	概率密度 $f(x)$	分布函数 $F(x)$	期望 $E(X)$	方差 $D(X)$
正态分布 $N(\mu,\sigma^2)$	$\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$	$\Phi(x)$	$\mu$	$\sigma^2$
均匀分布 $U(a,b)$	$\frac{1}{b-a}$	$\frac{x-a}{b-a}$	$\frac{a+b}{2}$	$\frac{(b-a)^2}{12}$
指数分布 $\exp(\lambda)$	$\lambda\mathrm e^{-\lambda x}$	$1-\mathrm e^{-\lambda x}$	$\frac{1}{\lambda}$	$\frac{1}{\lambda^2}$
卡方分布 $\chi^2(n)$	(Holy crap)	(Nope)	$n$	$2n$
t 分布 $t(n)$	(Don't do it)	(Gone)	$0$	(?)
F 分布 $F(n_1,n_2)$	(Well...)	(Sank)	(U guess)	(lol)
伽马分布 $\Gamma(\alpha,\beta)$	(LMAO)	(Blown)	$\frac{\alpha}{\beta}$	$\frac{\alpha}{\beta^2}$

正态分布

$X_i$ 独立分布于 $N(\mu_i,\sigma_i^2)$，$Z=\sum_{i}a_iX_i \sim N(\sum_ia_i\mu_i, \sum_ia_i^2\sigma_i^2)$

卡方分布

$\chi^2(2)\sim \exp(\frac{1}{2})$

$Z_1\sim\chi^2(n_1)$，$Z_2 \sim \chi^2(n_2)$，$Z_1+Z_2\sim \chi^2(n_1+n_2)$

$X_1,X_2,\cdots, X_n$ 独立同分布于 $N(0,1)$，$\sum_{i=1}^n X_i^2 \sim \chi^2(n)$

$X_1,X_2,\cdots, X_n$ 独立同分布于 $N(\mu,\sigma^2)$，$\frac{1}{\sigma^2}\sum_{i=1}^n (X_i-\mu)^2 \sim \chi^2(n)$

t 分布

$\lim_{n\to\infty}t(n)\to N(0,1)$

$X\sim N(0,1)$，$Y\sim \chi^2(n)$，$T=\frac{X}{\sqrt{Y/n}}\sim t(n)$

F 分布

$X\sim \chi^2(n_1)$，$Y\sim \chi^2(n_2)$，$F=\frac{X/n_1}{Y/n_2}\sim F(n_1, n_2)$

二维连续分布

二维正态分布

$N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$

其中 $\rho$ 为 $X$，$Y$ 的相关系数，$X\sim N(\mu_1,\sigma_1^2)$，$Y\sim N(\mu_2,\sigma_2^2)$

二维均匀分布

Soo EZ

大数定律

伯努利大数定律

对于伯努利试验

\[ \lim_{n\to\infty}\left\{\left|\frac{\eta_n}{n}-p\right|<\varepsilon\right\}=1 \] 切比雪夫大数定律在伯努利试验下的特殊情况

切比雪夫大数定律

两两不相关序列且方差一致有界，$\forall\ \varepsilon >0$

\[ \lim_{n\to\infty}P\left\{\left| \frac{1}{n}\sum_{i=1}^{n}X_i - \frac{1}{n}\sum_{i=1}^{n}E(X_i) \right|\geq\varepsilon\right\}=0 \]

独立同分布大数定律

切比雪夫大数定律在独立同分布下的特殊情况

辛钦大数定律

$\{X_n\}$ 独立同分布且期望 $\mu$ 存在有界（不要求方差存在），则 $\overline{X_n}\stackrel{P}{\longrightarrow} \mu$

中心极限定理

$\{X_n\}$ 独立同分布，期望 $\mu$、方差 $\sigma^2$ 存在

\[ \lim_{n\to\infty}P\left\{ \frac{\sum_{i=1}^n X_i-n\mu}{\sqrt{n}\sigma} \leq x\right\} = \Phi(x) \]

数理统计

统计量

设样本 $(X_1,X_2,\cdots,X_n)$ 为总体 $X$ 的样本

样本均值

\[ \overline X=\frac{1}{n}\sum_{i=1}^{n}X_i \]

若总体具有二阶矩，$E(\overline X)=\mu$，$D(\overline X)=\frac{\sigma^2}{n}$

是 $\mu$ 的无偏估计量

$\overline X^2$ 是 $\mu^2$ 的渐进无偏估计量

样本方差

\[ S^2=\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline X)^2 = \frac{1}{n-1}\left[\sum_{i=1}^n X_i^2-n\overline X ^2\right] \]

若总体具有二阶矩，$E(S^2)=\sigma^2$

是 $\sigma^2$ 的无偏估计量

样本标准差

\[ S=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(X_i-\overline X)^2} \]

样本 k 阶原点矩

\[ A_k=\frac{1}{n}\sum_{i=1}^{n}X_i^k \]

是 $\alpha_k$ 的无偏估计量

样本 k 阶中心矩

\[ B_k=\frac{1}{n}\sum_{i=1}^{n}(X_i-\overline X)^k \]

$B_2$ 是 $\sigma^2$ 的渐进无偏估计量

次序统计量

\[ X_{(1)},X_{(2)},\cdots ,X_{(n)} \]

样本极差

\[ X_{(n)}-X_{(1)} \]

正态总体抽样

设 $(X_1,X_2,\cdots, X_n)$ 是来自正态总体 $N(\mu,\sigma^2)$ 的样本

$\overline X\sim N\left(\mu,\frac{\sigma^2}{n}\right)$
$\frac{(n-1)S^2}{\sigma^2}\sim \chi^2(n-1)$
$\overline X$ 与 $X^2$ 独立
$T=\frac{\sqrt n (\overline X-\mu)}{S}\sim t(n-1)$

设 $(X_1,X_2,\cdots, X_n)$ 是来自正态总体 $N(\mu_1,\sigma_1^2)$ 的样本， $(Y_1,Y_2,\cdots, Y_n)$ 是来自正态总体 $N(\mu_2,\sigma_2^2)$ 的样本 \[ F=\frac{S_{1n_1}^2/\sigma_1^2}{S_{2n_2}^2/\sigma_2^2}\sim F(n_1-1,n_2-1) \] 且 \[ T=\frac{(\overline X-\overline Y)-(\mu_1-\mu_2)}{S_W\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}} \sim t(n_1+n_2-2) \] 其中 \[ S_W=\frac{(n_1-1)S_{1n_1}^2+(n_2-1)S_{2n_2}^2}{n_1+n_2-2} \]

点估计

矩估计

有 $k$ 个未知参数时，求 $k$ 阶原点矩 $\alpha_k$ 和样本 $k$ 阶原点矩 $A_k$；矩法方程 $A_k=\alpha_k$

极大似然估计

观测值 $(x_1,x_2,\cdots,x_n)$，似然函数 $L(\theta_1,\theta_2,\cdots,\theta_l)=\prod_{i=1}^n f(x_i;\theta_1,\theta_2,\cdots,\theta_l)$

取对数求导求使似然函数最大的参数

估计量性质

无偏性

\[ E(\hat \theta)=\theta \]

渐进无偏性 $\lim_{n\to\infty}E(\hat\theta)=\theta$

有效性

\[ D(\hat\theta_1)\leq D(\hat\theta_2) \]

则 $\theta_1$ 较 $\hat\theta_2$ 有效

相合性

相和估计量

\[ \hat\theta\stackrel{P}{\longrightarrow}\theta \] 或 $\forall\ \varepsilon >0$，$\lim_{n\to\infty}P\{|\hat\theta - \theta|<\varepsilon\} = 0$

均方相和估计量

\[ \hat\theta\stackrel{L^2}{\longrightarrow}\theta \] 或 $\lim_{n\to\infty}E^2(\hat\theta-\theta) = 0$

相合估计量的函数是参数的函数的相合估计

置信区间

分位数

上侧 $\alpha$ 分位数 $x_\alpha$ \[ P\{X>x_\alpha\}=1-F(x_\alpha)=\alpha \]

置信区间

置信上下界

（明明是同一张表……）

假设检验

原假设 $H_0$，备择假设 $H_1$

拒绝域：拒绝 $H_0$ 的范围；接受域：接受 $H_0$ 的范围

I 类错误概率 $\alpha(\mu)=P\{\text{ rejects}H_0|H_0\text{ is true}\}$

II 类错误概率 $\beta(\mu)=P\{\text{ accepts}H_0|H_0\text{ is false}\}$

显著性检验：犯第一类错误概率小于显著性水平 $\alpha$

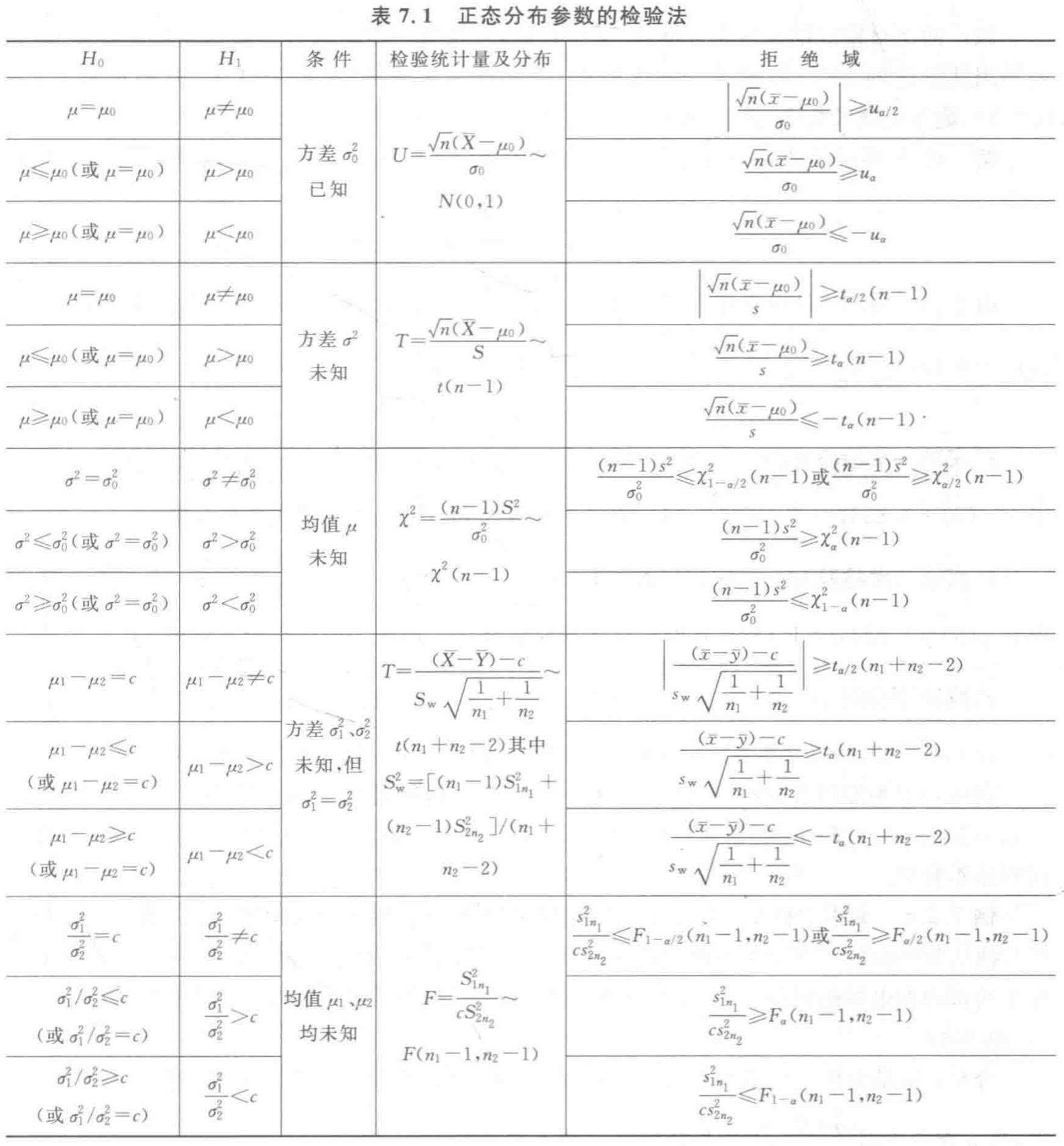
方差未知且不等的均值检验

一般先检验 $\sigma_1^2=\sigma_2^2$，题就有得做了

~~否则自行思考，然后发现没法做，继续睡觉~~

或者在大样本条件 $n_1\gg 1$，$n_2 \gg 1$ 下

统计量 \[ U=\frac{(\overline X-\overline Y)-c}{\sqrt{\dfrac{S_{1n_1}^2}{n_1}+\dfrac{S_{2n_2}^2}{n_2}}} \longrightarrow U(0,1) \]

下均值已知的方差检验

样本 $X_i$，$Y_i$ 来自总体已知均值分别为 $\mu_1$，$\mu_2$ 的分布

$H_0$：$\frac{\sigma_1^2}{\sigma_2^2}=c$，有统计量 \[ F=\frac{\frac{1}{n_1}\sum(X_i-\mu_1)^2}{c\frac{1}{n_2}\sum(Y_i-\mu_2)^2} \sim F(n_1,n_2) \]

随机过程

称随机变量族

\[ \{X(t,\omega),t\in T,\omega\in \Omega\} \] 为随机过程

固定 $\omega$ 时随机过程 $X(\ \cdot\ ,\omega)$ 称为样本函数

$T\in \mathbb{R}$ 称为指标集（参数集）

$\mathscr R(X)$ 称为状态集

有限维分布族

固定一个随机过程的一组 $t$ 得到一个随机变量族，分布函数 \[ F_X(x_1,x_2,\cdots;t_1,t_2,\cdots,t_n)=P\left(\bigcap_i\{X(t_i)\leq x_i\}\right) \] 称为有限维分布族

随机过程数字特征

均值函数

\[ m_X(t)=E(X(t)) \]

方差函数

\[ D_X(t)=D(X(t)) \]

自协方差函数

\[ C_X(t_1,t_2)=\mathrm{Cov}(X(t_1),X(t_2)) \]

自相关函数

\[ R_X(t_1,t_2)=E(X(t_1)X(t_2)) \]

互协方差函数

\[ C_{XY}(t_1,t_2)=\mathrm{Cov}(X(t_1),Y(t_2)) \]

互相关函数

\[ R_{XY}(t_1,t_2)=E(X(t_1)Y(t_2)) \]

随机过程分类

二阶矩过程

均值和方差对于任意参数均存在

正态过程（高斯过程）

任意有限维分布均为多维正态分布 \[ f(\boldsymbol x;\boldsymbol t)=(2\pi)^{-\frac{n}{2}}|\boldsymbol C|^{-\frac{1}{2}} \exp\left(-\frac{1}{2}(\boldsymbol x-\boldsymbol m)^\mathrm T\boldsymbol C^{-1}(\boldsymbol x-\boldsymbol m)\right) \] 其中

\[ \begin{align} \boldsymbol m&=(m_X(t_1),m_X(t_2),\cdots,m_X(t_n))^{\mathrm T} \nonumber \\ \boldsymbol C&= \begin{bmatrix} C_X(t_1,t_1) & C_X(t_1,t_2) & \cdots & C_X(t_1,t_n) \newline C_X(t_2,t_1) & C_X(t_2,t_2) & \cdots & C_X(t_2,t_n) \newline \vdots & \vdots & \ddots & \vdots \newline C_X(t_n,t_1) & C_X(t_n,t_2) & \cdots & C_X(t_n,t_n) \newline \end{bmatrix} \nonumber \end{align} \]

正交增量过程

若 $T=\{t|t>0\}$，$X(0)=0$，$s<t$

有 $R_X(s,t)=E(X^2(s))$

独立增量过程

对与任意时间列，增量两两不相关

平稳独立增量过程

增量的概率分布与此增量开始时刻无关

马尔可夫过程

某一时刻将来的分布与之前时刻的分布无关

计数过程

计数过程 $N(t)$ 表示时间 $[0,t)$ 内随机事件 $A$ 发生的次数

$N(t)\in \mathbb{N}$
$\forall\ 0<s<t\ ,\ N(s)\leq N(t)$

泊松过程

满足如下条件的计数过程 $N(t)$

$N(0)=0$
独立增量
$P\{N(t+s)-N(s)=k\}=P\{N(t)=k\}$（增量平稳性）
出现的概率与时间成伪线性：$P\{N(t+\Delta t)-N(t)=1\}=\lambda\Delta t-\mathrm o(\Delta t)$
同一时刻不会冒出两个来：$P\{N(t+\Delta t)-N(t)\geq 2\}=\mathrm o(\Delta t)$

称为强度为 $\lambda$ 的泊松过程

泊松分布性质 \[ P\{N(t)=k\}=\frac{(\lambda t)^k}{k!}\mathrm e^{-\lambda t} \] 到达时间性质

$S_n$ 表示第 $n$ 件事发生的时刻

\[ f_{S_n}(t)= \begin{cases} \frac{\lambda(\lambda t)^{n-1}}{(n-1)!}\mathrm e^{-\lambda t} &,\ t>0 \newline 0 &,\ t\leq 0 \end{cases} \]

特别的，$S_1\sim \exp(\lambda)$，且时间间隔序列 $T_i$ 独立同分布于 $\exp(\lambda)$，这也是计数过程是齐次泊松过程的充要条件

布朗运动/维纳过程

定义 ${W(t),t>0}$ 满足

$W(0)=0$
是独立增量过程
$W(t)-W(s)\sim N(0,\sigma^2|t-s|)$

性质：

是平稳独立增量过程
是正态过程
$m_W(t)=0$，$C_W(s,t)=R_W(s,t)=\sigma^2\min\{s,t\}$

均方意义下连续

\[ \lim_{\Delta t\to 0}E((X(t_0+t)-X(t_0))^2)=0 \]

记作

\[ \mathop{\mathrm{l.i.m.}}\limits_{\Delta t\to 0} X(t+\Delta t)=X(t) \]

平稳过程

严平稳过程

任何有限维分布函数不随时间推移（在参数集上平移）改变

宽平稳过程

均值函数是常数；自相关函数 $R_X(t_1,t_2)$ 只是时间差 $\tau=t_2-t_1$ 的函数 $R_X(\tau)$

即一阶矩与二阶矩不随时间推移改变

白噪声序列

自相关函数仅在 $\tau=0$ 为 $\sigma^2$，否则为零

宽平稳过程的性质

$R_X(\tau)=R_X(-\tau)$
$|R_X(\tau)|\leq R_X(0)$，$|C_X(\tau)|\leq C_X(0)$（由柯西不等式推导）
$R_X(\tau)$ 非负定

平稳相关

$X$，$Y$ 是两个平稳过程，若 $R_{XY}(t,t+\tau)=E(X(t)Y(t+\tau))=R_{XY}(\tau)$，则称其平稳相关

互协方差函数、互相关函数性质与自协方差函数、自相关函数类似

各态历经性

必须是平稳过程哦

时间均值

\[ \overline{X(t)}=\lim_{T\to+\infty}\frac{1}{2T}\int_{-T}^T X(t)\mathrm dt \]

它是一个随机变量，那么有期望和方差如下

\[ \begin{align} E(\overline{X(t)})&=m_X \nonumber\newline D(\overline{X(t)})&=\lim_{T\to+\infty}\frac{1}{T}\int_{0}^{2T} \left(1-\frac{\tau}{2T}\right)(R_X(\tau)-m_X^2)\mathrm d\tau \nonumber \end{align} \]

时间相关函数

\[ \overline{X(t)X(t+\tau)}=\lim_{T\to+\infty}\frac{1}{2T}\int_{-T}^T X(t)X(t+\tau)\mathrm dt \]

它是一个随机过程，且参数仅为 $\tau$，可写作 $\overline{Y_{\tau}(t)}$，说明时间相关函数是状态集表示时间均值的随机过程！

而且当 $\tau$ 固定时，$Y_{\tau}(t)$ 是一个平稳过程，有自相关函数与均值函数如下（注意平稳过程的均值函数是常数）

\[ \begin{align} R_{Y_{\tau}}(\tau_1)=R_\tau(\tau_1)=E(X(t)X(t+\tau)X(t+\tau_1)X(t+\tau_1+\tau)) \nonumber\newline m_{Y_{\tau}}=R_X(\tau)\nonumber \end{align} \]

那么随机过程 $Y(\tau)=\overline{Y_{\tau}(t)}$ 的均值函数和方差函数如下

\[ \begin{align} m_Y(\tau)&=E(Y(\tau))=R_X(\tau) \nonumber\newline D_Y(\tau)&=D(Y(\tau))=\lim_{T\to+\infty}\frac{1}{T}\int_{0}^{2T} \left(1-\frac{\tau_1}{2T}\right)(R_\tau(\tau_1)-R_X^2(\tau))\mathrm d\tau_1\nonumber \end{align} \]

均值各态历经性

定义 \[ P\left\{\overline{X(t)} = E(X(t)) = m_X\right\}=1 \] 充要条件 $D\left(\overline{X(t)}\right)=0$

充分条件 $\lim_{\tau\to\infty}R_X(\tau)=m_X^2$，即无穷远不相关

自相关函数各态历经性

定义 \[ P\left\{\overline{X(t)X(t+\tau)} = E(X(t)X(t+\tau)) = R_X(\tau)\right\}=1 \] 充要条件 $D_Y(\tau)\equiv 0$（但注意 $Y(\tau)$ 不是平稳过程，$m_Y(\tau)$ 也不是常数）

\(X\) 的分布	分布律 \(P\{x=k\}\)	期望 \(E(X)\)	方差 \(D(X)\)
两点分布 \(B(n,p)\)	\(C_n^kp^k(1-p)^{n-k}\)	\(np\)	\(np(1-p)\)
泊松分布 \(P(\lambda)\)	\(\frac{\lambda^k}{k!}\exp(-\lambda)\)	\(\lambda\)	\(\lambda\)
几何分布 \(G(p)\)	\((1-p)^{k-1}p\)	\(\frac{1}{p}\)	\(\frac{1-p}{p^2}\)

\(X\) 的分布	概率密度 \(f(x)\)	分布函数 \(F(x)\)	期望 \(E(X)\)	方差 \(D(X)\)
正态分布 \(N(\mu,\sigma^2)\)	\(\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)\)	\(\Phi(x)\)	\(\mu\)	\(\sigma^2\)
均匀分布 \(U(a,b)\)	\(\frac{1}{b-a}\)	\(\frac{x-a}{b-a}\)	\(\frac{a+b}{2}\)	\(\frac{(b-a)^2}{12}\)
指数分布 \(\exp(\lambda)\)	\(\lambda\mathrm e^{-\lambda x}\)	\(1-\mathrm e^{-\lambda x}\)	\(\frac{1}{\lambda}\)	\(\frac{1}{\lambda^2}\)
卡方分布 \(\chi^2(n)\)	(Holy crap)	(Nope)	\(n\)	\(2n\)
t 分布 \(t(n)\)	(Don't do it)	(Gone)	\(0\)	(?)
F 分布 \(F(n_1,n_2)\)	(Well...)	(Sank)	(U guess)	(lol)
伽马分布 \(\Gamma(\alpha,\beta)\)	(LMAO)	(Blown)	\(\frac{\alpha}{\beta}\)	\(\frac{\alpha}{\beta^2}\)