电路需记公式集锦
这个文档用来在考前清扫公式与部分定义,并不能有效地帮助理解,但是很有用
2021.1.7
数学基础
积化和差与和差化积
请不要尝试记住 8 个公式,反之启发式地从以下二式推导 \[ \begin{align} \cos(\alpha + \beta) &+ \cos(\alpha - \beta) \nonumber \newline &= \cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta) + \cos(\alpha)\cos(\beta) + \sin(\alpha)\sin(\beta) \nonumber \newline &= 2\cos(\alpha)\cos(\beta) \nonumber \newline \sin(\alpha+\beta) &+ \sin(\alpha - \beta) \nonumber \newline &= \sin(\alpha)\cos(\beta) + \sin(\beta)\cos(\alpha) + \sin(\alpha)\cos(\beta) - \sin(\beta)\cos(\alpha) \nonumber \newline &= 2\sin(\alpha)\cos(\beta) \nonumber \end{align} \]
周期量与复数
设周期量
\[ f(t) = A_m\cos\left(\frac{2\pi}{T}t+\phi\right) = A_m\cos\left(2\pi f t+\phi\right) = A_m\cos\left(\omega t+\phi\right) \]
其中 \(A_m\) 为最大值,\(\omega\) 为角频率,\(\phi\) 为初相角(\(|\phi|\leq \pi\))
平均值 \(f_{avg} \triangleq \frac{1}{T}\int_{t_0}^{t_0+T}|f|\mathrm dt=\frac{2}{\pi}A_m\)
有效值 \(f_{eff} \triangleq \sqrt{\frac{1}{T}\int_{t_0}^{t_0+T}f^2\mathrm dt}=\frac{\sqrt{2}}{2}A_m\)
周期量的复数形式 \(f(t) = \frac{1}{2}A_m\left[\mathrm e^{\mathrm i(\omega t + \phi)} + \mathrm e^{-\mathrm i(\omega t + \phi)}\right]\)
欧拉公式 \(\mathrm e^{\mathrm ix}=\cos x + \mathrm i\sin x\)
极坐标形式 \(r\mathrm e^{\mathrm i \theta} = r\angle\theta\)
傅里叶级数
\[ f(t)=\frac{a_0}{2}+\sum_{n=1}^{\infty}\left[a_n\cos(n\omega t)+b_n\sin(n\omega t)\right] \]
其中
\[ \begin{align} a_n&=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)\cos(n\omega t)\mathrm d t &,n\in \mathbb{Z}_+ \nonumber \\ b_n&=\frac{2}{T}\int_{t_0}^{t_0+T}f(t)\sin(n\omega t)\mathrm d t &,n\in \mathbb{Z}_+ \nonumber \end{align} \]
二阶常系数齐次线性微分方程
形式
\[ \frac{\mathrm d^2y}{\mathrm d x^2} + p\frac{\mathrm dy}{\mathrm d x}+qy=0 \]
特征方程
\[ \lambda^2 +p\lambda + q = 0 \]
特征根 \(\lambda_1,\lambda_2\),齐次方程通解如下
当 \(\lambda_1 \neq \lambda_2\) 为一对实根: \[ y(x)=C_1e^{\lambda_1 x}+C_2e^{\lambda_2 x} \]
当 \(\lambda_1 = \lambda_2 = \lambda\): \[ y(x)=(C_1+C_2x)e^{\lambda x} \]
当 \(\lambda = \alpha \pm \mathrm i\beta\): \[ y(x)=e^{\alpha x}(C_1\cos\beta x+C_2\sin\beta x) \]
等效
Y-Δ 变换(T-π 变换)
\[ \begin{align} \text{ Y impedences} &= \frac{\text{ product of adjacent} \Delta \text{ impedences}}{\text{ sum of}\Delta \text{ impedences}}\nonumber\newline \Delta \text{ impedences} &= \frac{\text{ sum of products of Y impedences}}{\text{ non-adjacent Y impedence}}\nonumber \end{align} \]
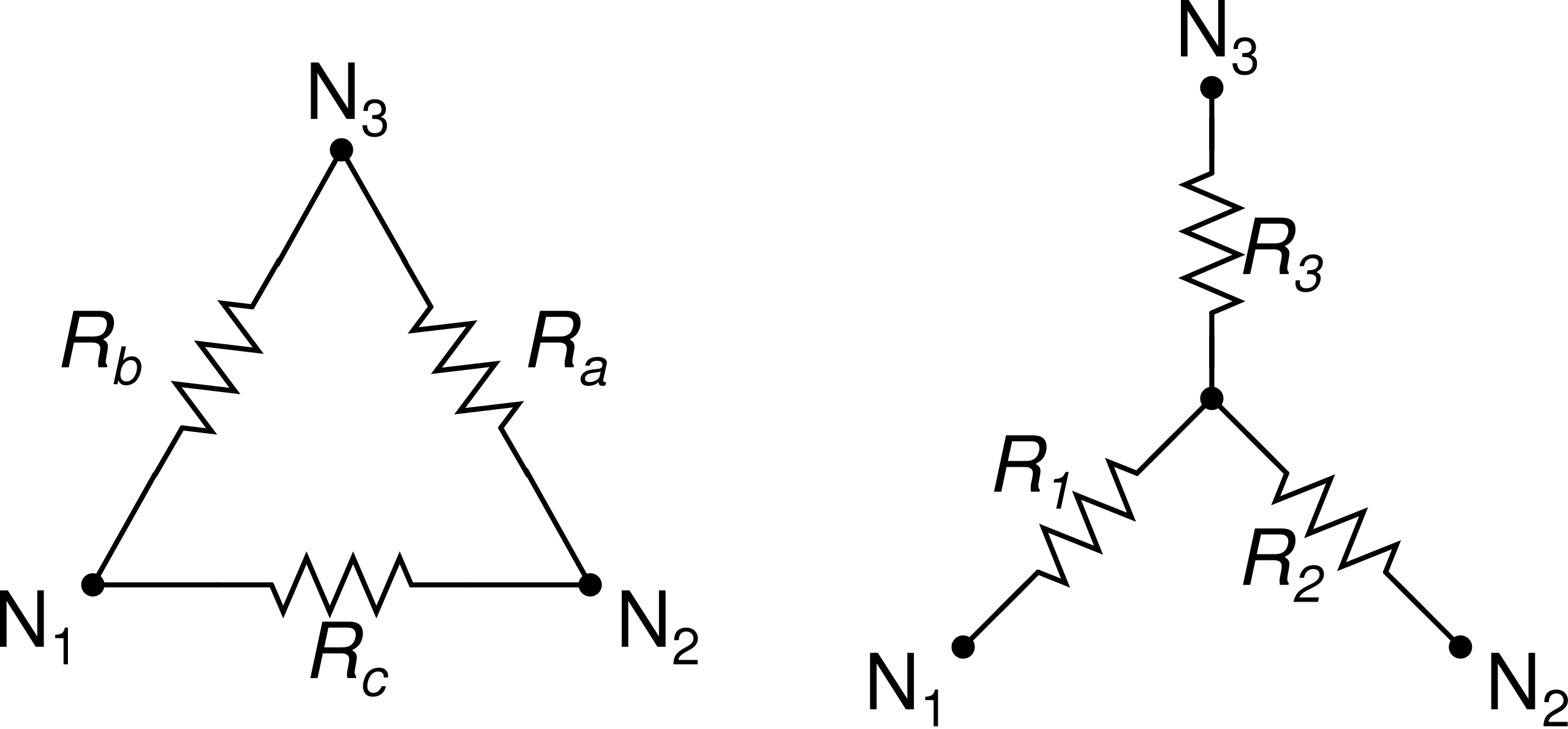
\[ \begin{align} R_1&=\frac{R_bR_c}{R_a+R_b+R_c} \nonumber\newline R_a&=\frac{R_1R_2 +R_2R_3+R_1R_3}{R_1}\nonumber \end{align} \]
最大功率传输定理
设负载阻抗 \(Z_L\) 连接于二端口等效戴维宁电路 \(\dot U_S, Z_S\)。当 \(Z_L = Z_S^*\) 时,有负载最大功率:
\[ P_{L max} = \frac{U_s^2}{4R_S} \]
电路的图
最大独立方程数
对结点数量 \(n\),支路数量 \(b\),的连通图有:
回路电流法方程数 \(=\) 独立 KVL 方程数 \(= b - (n-1)\)
结点电压法方程数 \(=\) 独立 KCL 方程数 \(= n-1\)
特勒根定理 2
如果两个电路的图 \(G = \hat G\),设各支路关联参考方向电流分别为 \((i_1, i_2, \cdots, i_b)\), \((\hat i_1, \hat i_2, \cdots, \hat i_b)\),电压分别为 \((u_1, u_2, \cdots, u_b)\), \((\hat u_1, \hat u_2, \cdots, \hat u_b)\),则有:
\[ \begin{cases} & \sum\limits_{k = 1}^b u_k \hat i_k = 0 \newline & \sum\limits_{k = 1}^b \hat u_k i_k = 0 \end{cases} \]
由特勒根定理 2 可推出特勒根定理 1(对同一个图)、互易定理(对一对激励响应互换图)。
特勒根定理 2 特例:当存在纯电阻 \(n\) 端口网络 \(N\subset G\),其中端口关联参考方向方向电流分别为 \((i_1, i_2, \cdots, i_n)\), \((\hat i_1, \hat i_2, \cdots, \hat i_n)\),电压分别为 \((u_1, u_2, \cdots, u_n)\), \((\hat u_1, \hat u_2, \cdots, \hat u_n)\),则有:
\[ \sum\limits_{k = 1}^n u_k \hat i_k = \sum\limits_{k = 1}^n \hat u_k i_k \]
元件性质
关联参考方向电压 \(u(t)\),电流 \(i(t)\),储能 \(W(t)\)。
电容
一极板上电荷量 \(q\) \[ \begin{align} q &= Cu \nonumber\newline i &= \frac{\mathrm dq}{\mathrm d t} = C \frac{\mathrm du}{\mathrm d t} \nonumber\newline u(t) &= u(t_0) + \frac{1}{C}\int_{t_0}^{t} i(\xi) \mathrm d \xi \nonumber\\ W(t) &= \frac{1}{2}C u^2(t) \nonumber \end{align} \] \(C_1, C_2\) 串联:\(C_{eq} = \frac{C_1C_2}{C_1+C_2}\),并联:\(C_{eq} = C_1 + C_2\)
阻抗 \(Z_C = \frac{1}{\mathrm j\omega C}\)
电感
电感磁链 \(\Psi\)
\[ \begin{align} \Psi &= Li \nonumber\newline u &= \frac{\mathrm d\Psi}{\mathrm d t} = L \frac{\mathrm di}{\mathrm d t} \nonumber\newline i(t) &= i(t_0) + \frac{1}{L}\int_{t_0}^{t} u(\xi) \mathrm d \xi\nonumber\\ W(t) &= \frac{1}{2}L i^2(t)\nonumber \end{align} \] \(L_1, L_2\)串联:\(L_{eq} = L_1 + L_2\),并联:\(L_{eq} = \frac{L_1L_2}{L_1+L_2}\)
阻抗 \(Z_L = \mathrm j\omega L\)
变压器
耦合因数 \(k=\frac{M}{\sqrt{L_1L_2}} \leq 1\)
理想变压器:\(L_1,L_2 \to \infty\),\(k = 1\),\(n = \frac{N_1}{N_2} = \frac{\sqrt{L_1}}{\sqrt{L_2}}\)
阻抗变换:\(Z_{11'}=n^2 Z_L\)
一阶电路
RC 一阶电路,时间常数 \(\tau \triangleq RC\)
RL 一阶电路,时间常数 \(\tau \triangleq \frac{L}{R}\)
全响应:\(f(t) = f(\infty)+[f(0_+)-f(\infty)]e^{-\frac{t}{\tau}}\)
二阶电路
RLC 串联电路的零输入响应
微分方程:
\[ LC\frac{\mathrm d^2u_C}{\mathrm d t^2} + RC\frac{\mathrm du_C}{\mathrm d t}+u_C=0 \]
特征根:
\[ p = -\frac{R}{2L}\pm \sqrt{\left(\frac{R}{2L}\right)^2-\frac{1}{LC}} \]
形式解:
\[ \begin{cases} & u_C \text{ Over damping} & , R > 2\sqrt{\frac{L}{C}}; \newline & u_C \text{ Critical damping} & , R = 2\sqrt{\frac{L}{C}}; \newline & u_C \text{ Underdamping} & , R < 2\sqrt{\frac{L}{C}}. \end{cases} \]
利用阶跃响应求冲激响应
设线性电路阶跃响应 \(s(t)\),冲激响应 \(h(t)\),有 \(h(t) = \frac{\mathrm d s(t)}{\mathrm d t}\)
利用阶跃函数求复合阶跃响应
求复合形式、分别求解、叠加。(卷积求解的特例)
利用卷积求任意激励响应
设激励函数 \(e(t)\),响应 \(r(t)\),冲激响应 \(h(t)\)
\[ r(t) = e(t)*h(t) = \int_0^t e(\xi)h(t - \xi) \mathrm d\xi \]
正弦稳态电路与相量法
阻抗角 \(\phi_Z = \phi_u - \phi_i\)
功率
有功功率 \(P \triangleq UI\cos\phi_Z\),单位 W(瓦);
无功功率 \(Q\triangleq UI\sin\phi_Z\),单位 var(乏);
视在功率 \(S\triangleq UI\),单位 \(\mathrm V\cdot \mathrm A\)(伏安);
复功率 \(\bar S \triangleq \dot U \dot I^*=UI\angle\phi_z=P+\mathrm jQ = I^2Z=U^2Y^*\),单位 \(\mathrm V\cdot \mathrm A\)(伏安)。
功率因数 \(\lambda=\cos\phi_Z = \frac{P}{S}\)
谐振
电流电压同相位
RLC 串联电路谐振
- 谐振角频率 \(\omega_0 = \frac{1}{\sqrt{LC}}\)
- 品质因数 \(Q\triangleq \frac{\omega_0 L}{R} = \frac{1}{R}\sqrt{\frac{L}{C}} = \frac{U_C(\mathrm j \omega_0)}{U_S(\mathrm j\omega_0)}\)
- 带宽 \(BW\):\(|H_R(\mathrm j\eta)|\geq \frac{1}{\sqrt{2}}\),\(BW = \Delta \omega = \frac{\omega_0}{Q}\)
GLC 并联电路谐振
- 谐振角频率 \(\omega_0 = \frac{1}{\sqrt{LC}}\)
- 品质因数 \(Q\triangleq \frac{\omega_0 C}{G} = \frac{1}{G}\sqrt{\frac{C}{L}} = \frac{I_L(\mathrm j \omega_0)}{I_S(\mathrm j\omega_0)}\)
- 带宽 \(BW\):\(|H_R(\mathrm j\eta)|\geq \frac{1}{\sqrt{2}}\),\(BW = \Delta \omega = \frac{\omega_0}{Q}\)
三相电路
三相:ABC 依次滞后 \(\frac{2}{3}\pi\)
线电流:\(\dot I_A,\dot I_B,\dot I_C,\dot I_N\) 为输电线电流
线电压:\(\dot U_{AB},\dot U_{BC},\dot U_{CA}\) 为线间电压
相电流:\(\dot I_{AB},\dot I_{BC},\dot I_{CA}\) 为线间电流
相电压:\(\dot U_A,\dot U_B,\dot U_C\) 为线到中性线电压
二瓦计法:\(P=\mathrm{Re}[\dot U_{AC}\dot I_A^* + \dot U_{BC}\dot I_B^*]\)
非正弦周期电流电路
设 \(i(t) = I_0 + \sum\limits_{k=1}^\infty \sqrt{2}I_{k}\cos(k\omega_1 t+\phi_{ik})\),\(u(t) = U_0 + \sum\limits_{k=1}^\infty \sqrt{2}U_{k}\cos(k\omega_1 t+\phi_{uk})\),\(\phi_k = \phi_{uk} - \phi_{ik}\)
有效值:
- 电流 \(I = \sqrt{I_0^2 + \sum\limits_{k=1}^\infty I_{k}^2}\)
- 电压 \(U = \sqrt{U_0^2 + \sum\limits_{k=1}^\infty U_{k}^2}\)
- 功率 \(P = U_0I_0 + \sum\limits_{k=1}^\infty U_kI_k \cos\phi_k\)
二端口网络
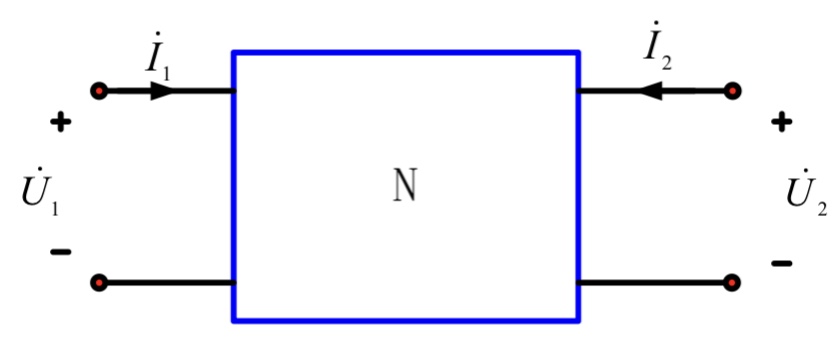
Y 参数:短路导纳参数
\[ \begin{bmatrix} \dot I_1 \newline \dot I_2 \end{bmatrix} =\mathbf Y \begin{bmatrix} \dot U_1 \newline \dot U_2 \end{bmatrix} = \begin{bmatrix} Y_{11} & Y_{12} \newline Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix} \dot U_1 \newline \dot U_2 \end{bmatrix} \]
Z 参数:开路阻抗参数
\[ \begin{bmatrix} \dot U_1 \newline \dot U_2 \end{bmatrix} =\mathbf Z \begin{bmatrix} \dot I_1 \newline \dot I_2 \end{bmatrix} = \begin{bmatrix} Z_{11} & Z_{12} \newline Z_{21} & Z_{22} \end{bmatrix} \begin{bmatrix} \dot I_1 \newline \dot I_2 \end{bmatrix} \]
T 参数:传输参数
\[ \begin{bmatrix} \dot U_1 \newline \dot I_1 \end{bmatrix} =\mathbf T \begin{bmatrix} \dot U_2 \newline -\dot I_2 \end{bmatrix} = \begin{bmatrix} A & B \newline C & D \end{bmatrix} \begin{bmatrix} \dot U_2 \newline -\dot I_2 \end{bmatrix} \]
H 参数:混合参数
\[ \begin{bmatrix} \dot U_1 \newline \dot I_2 \end{bmatrix} =\mathbf H \begin{bmatrix} \dot I_1 \newline \dot U_2 \end{bmatrix} = \begin{bmatrix} H_{11} & H_{12} \newline H_{21} & H_{22} \end{bmatrix} \begin{bmatrix} \dot I_1 \newline \dot U_2 \end{bmatrix} \]